Data structures are nothing different. They are like the bookshelves of your application where you can organize your data. Different data structures will give you different facility and benefits. To properly use the power and accessibility of the data structures you need to know the trade-offs of using one.
不同的数据结构有不同的适用场景和优缺点,你需要仔细权衡自己的需求之后妥善适用它们
布隆过滤器就是践行这句话的代表
什么是布隆过滤器
布隆过滤器本质上是一种数据结构,比较巧妙的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 某样东西一定不存在或者可能存在。
相比于传统的 List、Set、Map 等数据结构,它更高效、占用空间更少,但是缺点是其返回的结果是概率性的,而不是确切的。
优点:
不需要存储 key ,空间占用很小
高效地插入和查询缺点:
返回具有不确定性
元素删除相对困难
布隆过滤器的原理
假设有个集合 A,A 中有 n 个元素。利用 k 个哈希散列函数,将 A 中的每个元素映射到一个长度为 a 位的数组 B 中的不同位置上,这些位置上的二进制数均设置为 1 。如果待检查的元素,经过这 k 个哈希散列函数的映射后,发现其 k 个位置上的二进制数全部为 1 ,这个元素很可能属于集合 A ,反之,一定不属于集合 A。
布隆过滤器的数据结构
布隆过滤器是一个 bit 向量或者说 bit 数组:
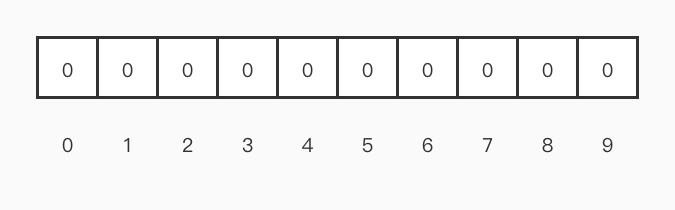
如果要映射一个 key 值到布隆过滤器中,需要使用多个不同的哈希函数生成多个哈希值,并对每个生成的哈希值指向的 bit 位置 1,例如针对值 Chinese 和三个不同的哈希函数分别生成了哈希值 1、4、7,则数据结构状态转变为:
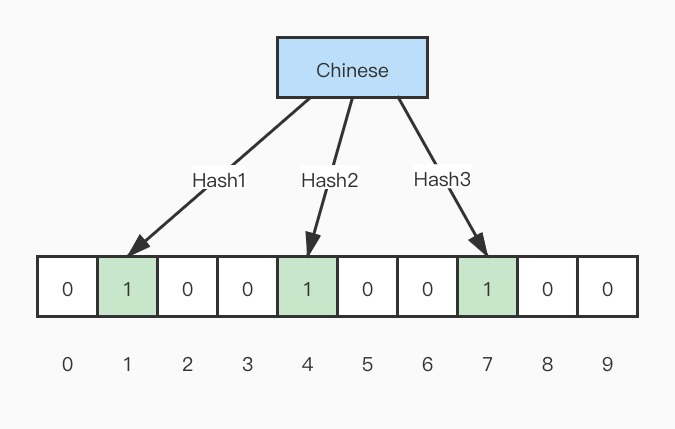
现在再存一个 key 值为 English,三个哈希函数返回值分别是 2、4、8 ,则数据结构继续变为:
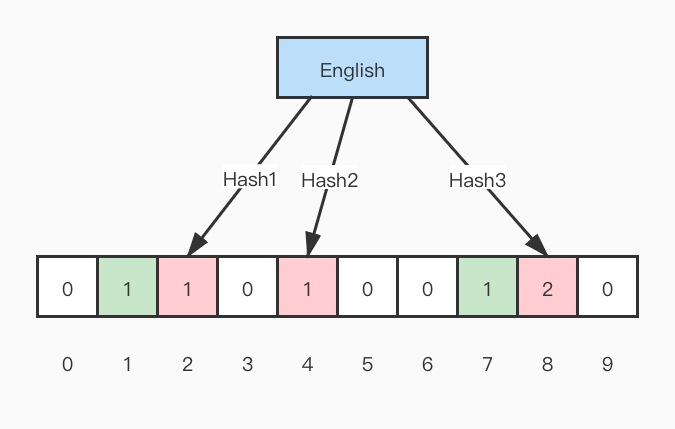
值得注意的是,4 这个 bit 位由于两个值的哈希函数都返回了这个 bit 位,因此它被覆盖了。
现在,
- 查询 Math 这个 key 值是否存在,如果三个哈希函数返回了 1、5、8 三个值,因为 5 这个 bit 位上的值为 0,说明没有任何一个值映射到这个 bit 位上,因此可以很确定地说 Math 这个 key 值不存在。
- 查询 Physics 这个 key 值是否存在,如果三个哈希函数返回了 1、7、8,检查发现这三个 bit 位上的值均为 1,那么可以说 Physics 存在了么?答案是不可以,只能是 Physics 这个 key 值可能存在。
因为随着增加的值越来越多,被置为 1 的 bit 位也会越来越多,这样某个值 Chemistry 即使没有被存储过,但是万一哈希函数返回的三个 bit 位都被其他值置位了 1 ,那么程序还是会判断 Chemistry 这个值存在。
算法
- 首先需要 k 个 hash 函数,每个函数可以把 key 散列成为 1 个整数。
- 初始化时,需要一个长度为 n 比特的数组,每个比特位初始化为 0。
- 某个 key 加入集合时,用 k 个 hash 函数计算出k个散列值,并把数组中对应的比特位置为 1。
- 判断某个 key 是否在集合时,用 k 个 hash 函数计算出 k 个散列值,并查询数组中对应的比特位,如果所有的比特位都是 1 ,认为在集合中。
支持删除吗
传统的布隆过滤器并不支持删除操作。但是名为 Counting Bloom filter 的变种可以用来测试元素计数个数是否绝对小于某个阈值,它支持元素删除。
如何选择哈希函数个数和布隆过滤器长度
很显然,过小的布隆过滤器很快所有的 bit 位均为 1,那么查询任何值都会返回“可能存在”,起不到过滤的目的了。布隆过滤器的长度会直接影响误报率,布隆过滤器越长其误报率越小。
另外,哈希函数的个数也需要权衡,个数越多则布隆过滤器 bit 位置位 1 的速度越快,且布隆过滤器的效率越低;但是如果太少的话,那么误报率会变高。
k 为哈希函数个数,m 为布隆过滤器长度,n 为插入的元素个数,p 为误报率
如何选择适合业务的 k 和 m 值:
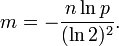
布隆过滤器误报率 p 与位数组大小 m 和集合中插入元素个数 n 的关系图:
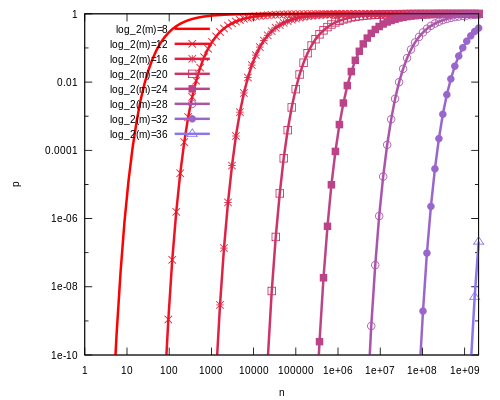
最佳实践
常见的适用常见有,利用布隆过滤器减少磁盘 IO 或者网络请求,因为一旦一个值必定不存在的话,可以不用进行后续昂贵的查询请求。
另外,既然使用布隆过滤器来加速查找和判断是否存在,那么性能很低的哈希函数不是个好选择,推荐 MurmurHash、Fnv 这些。
目前布隆过滤器已经有相应实现的开源类库啦,如 Google 的 Guava 类库,Twitter 的 Algebird 类库,信手拈来即可,或者基于 Redis 自带的 Bitmaps 自行实现设计也是可以的。
大 Value 拆分
Redis 因其支持 setbit 和 getbit 操作,且纯内存性能高等特点,因此天然就可以作为布隆过滤器来使用。但是布隆过滤器的不当使用极易产生大 Value,增加 Redis 阻塞风险,因此生成环境中建议对体积庞大的布隆过滤器进行拆分。
拆分的形式方法多种多样,但是本质是不要将 Hash(Key) 之后的请求分散在多个节点的多个小 bitmap 上,而是应该拆分成多个小 bitmap 之后,对一个 Key 的所有哈希函数都落在这一个小 bitmap 上。
